Kunci Jawaban TVRI 5 Mei 2020 SMA

Soal dan Jawaban TVRI 5 Mei 2020 SMA Kelas 10, 11, 12 – Kembali lagi dalam program Belajar dari Rumah TVRI yang tak terasa sudah memasuki Minggu ke-4.

Dalam materi soal TVRI 5 Mei 2020 untuk siswa-siswi SMA/ SMK sederajat ini, teman-teman akan belajar Matematika mengenai Sketsa Grafik Fungsi Kuadrat.

Sebelum tayangan berlangsung, siapkan dulu peralatan tulis teman-teman untuk mencatat hal-hal penting yang disampaikan dalam program tersebut.

Baca juga :

• Soal dan Jawaban TVRI 6 Mei 2020 SMA
• Soal dan Jawaban TVRI 5 Mei 2020 SMP
• Jadwal, Soal, Jawaban TVRI 4, 5, 6, 7, 8 Mei 2020

Diharapkan setelah menyimak materi hari ini, para siswa bisa memodelkan fenomena hubungan antara dua besaran dengan menggunakan fungsi kuadrat.

Oke tanpa panjang lebar lagi langsung saja kita simak soal dan jawaban TVRI 5 Mei 2020 SMA/ SMK selengkapnya.

Soal dan Jawaban TVRI 5 Mei 2020 SMA Kelas 10, 11, 12

Pertanyaan :

1. Diketahui fungsi y = x2 – 4x + 3

Tentukan:

• a. Titik potong kurva fungsi dengan sumbu-sumbu koordinat.
• b. Koordinat titik balik minimum.

—————————–

2. Gambar sketsa grafik fungsi berikut: y = -(x-3)² + 1

—————————–

Jawaban :

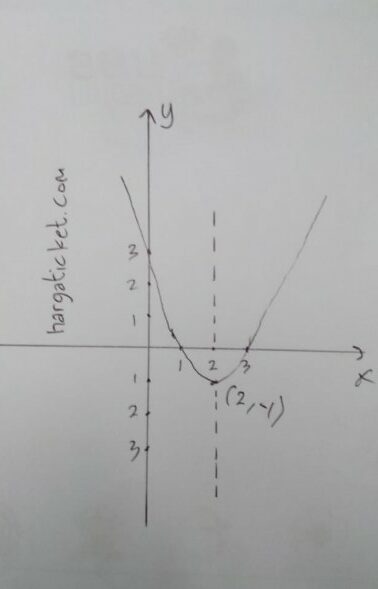
1. a. Titik potong pada sumbu y saat x = 0
y = x² – 4x + 3
y = 0 – 0 + 3
y = 3

Titik potong pada sumbu x saat y = 0
y = x² – 4x + 3
x² – 4x + 3 = 0
(x – 1)(x – 3) = 0
maka, x = 1 dan x = 3

Jadi titik potong HP {(0,3), (1,0), (3,0)}

b. Rumus titik balik minimum adalah x = ^-b⁄_2a

y = x² – 4x + 3
a = 1, b = -4, c = 3

x = ^-(-4)⁄₂₍₁₎
x = 2

y = 2.2 – 4.2 + 3
y = -1

Jadi koordinat titik balik minimum adalah (2,-1), bisa dilihat pada gambar

—————————–

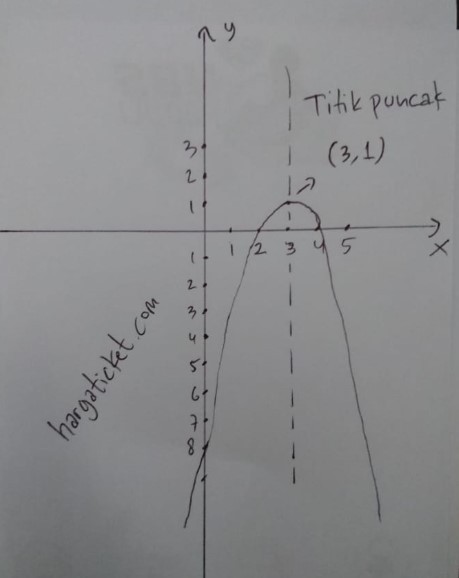
2. Berikut sketsa grafik fungsi : y = -(x-3)² + 1

Penjelasan :

y = -(x-3)² + 1
y = – (x² – 6x + 9) + 1
y = -x² + 6x – 9 + 1
y = -x² + 6x – 8

Sekarang kita mencari akar-akar dari persamaan di atas
y = -x² + 6x – 8 = 0
-x² + 6x – 8 = 0 (dikali minus)
x² – 6x + 8 = 0
(x – 4)(x – 2)
maka, x = 4 dan x = 2

Jadi titik potong dengan sumbu x adalah (4 , 0) dan (2 , 0)

Puncak grafik =
x = ^-b⁄_2a = ^-6⁄_2(-1)
x = 3

Masukkan nilai x pada persamaan soal di atas
y = -(x-3)² + 1
y = -(3-3)² + 1
y = -0 + 1
y = 1

Jadi titik puncak adalah (3,1)

Titik potong sumbu y saat x = 0, maka
y = -(x-3)² + 1
y = -(0-3)² + 1
y = -9 + 1
y = -8
Jadi titik potong sumbu y adalah (0,-8)

—————————–

Bagaimana sobat semua, sudah paham dengan materinya? Meskipun lumayan susah, tapi kalian gak boleh patah semangat ya, dan harus makin rajin belajar.

Jangan lupa ya share soal dan jawaban TVRI 5 Mei 2020 untuk siswa-siswi SMA ini ke sahabat kalian yang lain bisa melalui Whatsapp maupun Facebook, sampai jumpa.

sumber : hargaticket.com